在 Java 中计算互信息以选择训练集
场景
我正在尝试对 Java GUI 应用程序中的数据集实施监督学习。用户将获得要检查的项目或“报告”列表,并根据一组可用标签对其进行标记。一旦监督学习完成,标记的实例将被提供给学习算法。这将尝试根据用户想要查看其余项目的可能性对它们进行排序。
为了充分利用用户的时间,我想预先选择将提供有关整个报告集合的最多信息的报告,并让用户对它们进行标记。据我了解,要计算此值,有必要找到每个报告的所有互信息值的总和,并按该值对它们进行排序。然后,来自监督学习的标记报告将用于形成贝叶斯网络,以查找每个剩余报告的二进制值的概率。
示例
在这里,一个人为的示例可能有助于解释,并且当我无疑使用了错误的术语时可能会消除混乱:-) 考虑一个应用程序向用户显示新闻报道的示例。它根据用户显示的偏好选择首先显示哪些新闻报道。具有相关性的新闻报道的特征是原产国、类别或日期。因此,如果用户将来自苏格兰的单个新闻报道标记为有趣,它就会告诉机器学习者来自苏格兰的其他新闻报道对该用户感兴趣的可能性会增加。对于诸如“体育”之类的类别或诸如 2004 年 12 月 12 日之类的日期,类似。
可以通过为所有新闻报道选择任何顺序(例如按类别、按日期)或随机排序它们,然后随着用户的进行计算偏好来计算此偏好沿着。我想做的是让用户查看少量特定的新闻报道并说出他们是否对它们感兴趣(监督学习部分),从而在该排序上获得某种“领先优势”。要选择向用户展示哪些故事,我必须考虑整个故事集。这就是互信息的用武之地。对于每个故事,我想知道当用户对其进行分类时,它可以告诉我多少关于所有其他故事的信息。例如,如果有大量来自苏格兰的故事,我想让用户对其中(至少)其中一个进行分类。其他相关功能(例如类别或日期)也类似。目标是找到分类后能提供有关其他报告最多信息的报告示例。
问题
因为我的数学有点生疏,而且我是机器学习的新手,所以在将互信息的定义转换为 Java 中的实现时遇到了一些麻烦。维基百科将互信息方程描述为:
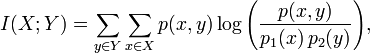
但是,我不确定如果这实际上可以在没有任何分类并且学习算法还没有计算任何内容的情况下使用。
正如在我的示例中,假设我有大量此类的新的、未标记的实例:
public class NewsStory {
private String countryOfOrigin;
private String category;
private Date date;
// constructor, etc.
}
在我的特定场景中,字段/特征之间的相关性基于完全匹配,因此,例如,一个天和 10 年的日期差异在不平等上是等效的。
相关性因素(例如,日期比类别更相关吗?)不一定相等,但它们可以是预定义的且恒定的。这是否意味着函数 p(x,y) 的结果是预定义值,还是我混淆了术语?
问题 (最后)
考虑到这个(假的)新闻故事示例,我该如何实施互信息计算?库、javadoc、代码示例等都是受欢迎的信息。此外,如果这种方法从根本上来说是有缺陷的,那么解释为什么会出现这种情况也将是一个同样有价值的答案。
附言。我知道 Weka 和 Apache Mahout 等库,所以仅仅提及它们对我来说并没有多大用处。我仍在搜索这两个库的文档和示例,专门寻找有关互信息的内容。真正对我有帮助的是指向资源(代码示例、javadoc),这些库可以在其中提供相互信息。
Scenario
I am attempting to implement supervised learning over a data set within a Java GUI application. The user will be given a list of items or 'reports' to inspect and will label them based on a set of available labels. Once the supervised learning is complete, the labelled instances will then be given to a learning algorithm. This will attempt to order the rest of the items on how likely it is the user will want to view them.
To get the most from the user's time I want to pre-select the reports that will provide the most information about the entire collection of reports, and have the user label them. As I understand it, to calculate this, it would be necessary to find the sum of all the mutual information values for each report, and order them by that value. The labelled reports from supervised learning will then be used to form a Bayesian network to find the probability of a binary value for each remaining report.
Example
Here, an artificial example may help to explain, and may clear up confusion when I've undoubtedly used the wrong terminology :-) Consider an example where the application displays news stories to the user. It chooses which news stories to display first based on the user's preference shown. Features of a news story which have a correlation are country of origin, category or date. So if a user labels a single news story as interesting when it came from Scotland, it tells the machine learner that there's an increased chance other news stories from Scotland will be interesting to the user. Similar for a category such as Sport, or a date such as December 12th 2004.
This preference could be calculated by choosing any order for all news stories (e.g. by category, by date) or randomly ordering them, then calculating preference as the user goes along. What I would like to do is to get a kind of "head start" on that ordering by having the user to look at a small number of specific news stories and say if they're interested in them (the supervised learning part). To choose which stories to show the user, I have to consider the entire collection of stories. This is where Mutual Information comes in. For each story I want to know how much it can tell me about all the other stories when it is classified by the user. For example, if there is a large number of stories originating from Scotland, I want to get the user to classify (at least) one of them. Similar for other correlating features such as category or date. The goal is to find examples of reports which, when classified, provide the most information about the other reports.
Problem
Because my math is a bit rusty, and I'm new to machine learning I'm having some trouble converting the definition of Mutual Information to an implementation in Java. Wikipedia describes the equation for Mutual Information as:
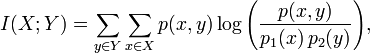
However, I'm unsure if this can actually be used when nothing has been classified, and the learning algorithm has not calculated anything yet.
As in my example, say I had a large number of new, unlabelled instances of this class:
public class NewsStory {
private String countryOfOrigin;
private String category;
private Date date;
// constructor, etc.
}
In my specific scenario, the correlation between fields/features is based on an exact match so, for instance, one day and 10 years difference in date are equivalent in their inequality.
The factors for correlation (e.g. is date more correlating than category?) are not necessarily equal, but they can be predefined and constant. Does this mean that the result of the function p(x,y) is the predefined value, or am I mixing up terms?
The Question (finally)
How can I go about implementing the mutual information calculation given this (fake) example of news stories? Libraries, javadoc, code examples etc. are all welcome information. Also, if this approach is fundamentally flawed, explaining why that is the case would be just as valuable an answer.
PS. I am aware of libraries such as Weka and Apache Mahout, so just mentioning them is not really useful for me. I'm still searching through documentation and examples for both these libraries looking for stuff on Mutual Information specifically. What would really help me is pointing to resources (code examples, javadoc) where these libraries help with mutual information.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(2)
我猜你的问题是这样的......
“给定一个未标记示例的列表,按照如果用户标记示例并将其添加到训练集中模型的预测准确性将提高多少来对列表进行排序。”
如果是这种情况,我认为互信息不是正确的选择,因为您无法计算两个实例之间的 MI。 MI 的定义是随机变量,单个实例不是随机变量,它只是一个值。
特征和类别标签可以被视为随机变量。也就是说,它们在整个数据集中具有值分布。您可以计算两个特征之间的互信息,以查看一个特征与另一个特征之间的“冗余”程度,或者计算一个特征与类标签之间的互信息,以了解该特征对预测的帮助程度。这就是人们通常在监督学习问题中使用互信息的方式。
我认为 ferdystschenko 关于主动学习方法的建议是一个很好的建议。
为了回应 Grundlefleck 的评论,我将通过使用他的 Java 对象类比思想来更深入地了解术语......
总的来说,我们使用术语“实例”、“事物”、“报告”和“示例”来指的是被分类的对象。让我们将这些东西视为 Java 类的实例(我省略了样板构造函数):
机器学习中的常用术语是 e1 是一个示例,所有示例都有两个特征 f1 和 f2,对于 e1,f1 的值为“foo”,f2 的值为“bar”。示例的集合称为数据集。
取数据集中所有样本的f1的所有值,这是一个字符串列表,也可以认为是一个分布。我们可以将该特征视为随机变量,并且列表中的每个值都是从该随机变量中获取的样本。例如,我们可以计算 f1 和 f2 之间的 MI。伪代码类似于:
<代码>
然而你不能计算 e1 和 e2 之间的 MI,它只是没有这样定义。
I am guessing that your problem is something like...
"Given a list of unlabeled examples, sort the list by how much the predictive accuracy of the model would improve if the user labelled the example and added it to the training set."
If this is the case, I don't think mutual information is the right thing to use because you can't calculate MI between two instances. The definition of MI is in terms of random variables and an individual instance isn't a random variable, it's just a value.
The features and the class label can be though of as random variables. That is, they have a distribution of values over the whole data set. You can calculate the mutual information between two features, to see how 'redundant' one feature is given the other one, or between a feature and the class label, to get an idea of how much that feature might help prediction. This is how people usually use mutual information in a supervised learning problem.
I think ferdystschenko's suggestion that you look at active learning methods is a good one.
In response to Grundlefleck's comment, I'll go a bit deeper into terminology by using his idea of a Java object analogy...
Collectively, we have used the term 'instance', 'thing', 'report' and 'example' to refer to the object being clasified. Let's think of these things as instances of a Java class (I've left out the boilerplate constructor):
The usual terminology in machine learning is that e1 is an example, that all examples have two features f1 and f2 and that for e1, f1 takes the value 'foo' and f2 takes the value 'bar'. A collection of examples is called a data set.
Take all the values of f1 for all examples in the data set, this is a list of strings, it can also be thought of as a distribution. We can think of the feature as a random variable and that each value in the list is a sample taken from that random variable. So we can, for example, calculate the MI between f1 and f2. The pseudocode would be something like:
However you can't calculate MI between e1 and e2, it's just not defined that way.
我知道信息增益仅与决策树(DT)有关,在决策树的构造中,对每个节点进行的分割是最大化信息增益的分割。 DT 是在 Weka 中实现的,因此您可以直接使用它,尽管我不知道 Weka 是否允许您计算 DT 节点下任何特定分割的信息增益。
除此之外,如果我理解正确的话,我认为您想要做的事情通常被称为
通过您编辑后的问题,我想我开始明白您的目标是什么。如果你想要的是计算 MI,那么在我看来,StompChicken 的答案和伪代码再清楚不过了。我还认为 MI 不是您想要的,您正在尝试重新发明轮子。
让我们概括一下:您希望训练一个可由用户更新的分类器。这是主动学习的经典案例。但为此,您需要一个初始分类器(您基本上可以只给用户随机数据进行标记,但我认为这不是一个选项)并且为了训练您的初始分类器,您至少需要一些少量的标记训练用于监督学习的数据。但是,您拥有的只是未标记的数据。你能用这些做什么?
好吧,您可以使用提供的标准聚类算法之一将它们聚类到相关实例组中通过 Weka 或某些特定的聚类工具,例如 Cluto。如果您现在获取每个集群的 x 个最中心的实例(x 取决于集群的数量和用户的耐心),并让用户将其标记为感兴趣或不感兴趣,您可以为其他实例采用此标签该集群也是如此(或者至少对于中心集群而言)。瞧,现在您有了训练数据,您可以使用这些数据来训练您的初始分类器,并通过每次用户将新实例标记为有趣或不感兴趣时更新分类器来启动主动学习过程。我认为你试图通过计算 MI 来实现的目标本质上是相似的,但可能只是你的收费方式错误。
不知道您的场景的详细信息,我应该认为您甚至可能根本不需要任何标记数据,除非您对标签本身感兴趣。只需对数据进行一次聚类,让用户从所有聚类的中心成员中选择一个他/她感兴趣的项目,并建议所选聚类中可能也有趣的其他项目。还建议来自其他集群的一些随机实例,这样,如果用户选择其中之一,您可能会认为相应的集群通常也很有趣。如果存在矛盾,并且用户喜欢集群中的某些成员,但不喜欢同一集群中的其他成员,那么您会尝试将数据重新集群到更细粒度的组中,以区分好与坏的组。甚至可以通过从一开始就使用分层聚类并在每个矛盾的用户输入原因时沿着聚类层次结构向下移动来避免重新训练步骤。
I know information gain only in connection with decision trees (DTs), where in the construction of a DT, the split to make on each node is the one which maximizes information gain. DTs are implemented in Weka, so you could probably use that directly, although I don't know if Weka lets you calculate information gain for any particular split underneath a DT node.
Apart from that, if I understand you correctly, I think what you're trying to do is generally referred to as active learning. There, you first need some initial labeled training data which is fed to your machine learning algorithm. Then you have your classifier label a set of unlabeled instances and return confidence values for each of them. Instances with the lowest confidence values are usually the ones which are most informative, so you show these to a human annotator and have him/her label these manually, add them to your training set, retrain your classifier, and do the whole thing over and over again until your classifier has a high enough accuracy or until some other stopping criterion is met. So if this works for you, you could in principle use any ML-algorithm implemented in Weka or any other ML-framework as long as the algorithm you choose is able to return confidence values (in case of Bayesian approaches this would be just probabilities).
With your edited question I think I'm coming to understand what your aiming at. If what you want is calculating MI, then StompChicken's answer and pseudo code couldn't be much clearer in my view. I also think that MI is not what you want and that you're trying to re-invent the wheel.
Let's recapitulate: you would like to train a classifier which can be updated by the user. This is a classic case for active learning. But for that, you need an initial classifier (you could basically just give the user random data to label but I take it this is not an option) and in order to train your initial classifier, you need at least some small amount of labeled training data for supervised learning. However, all you have are unlabeled data. What can you do with these?
Well, you could cluster them into groups of related instances, using one of the standard clustering algorithms provided by Weka or some specific clustering tool like Cluto. If you now take the x most central instances of each cluster (x depending on the number of clusters and the patience of the user), and have the user label it as interesting or not interesting, you can adopt this label for the other instances of that cluster as well (or at least for the central ones). Voila, now you have training data which you can use to train your initial classifier and kick off the active learning process by updating the classifier each time the user marks a new instance as interesting or not. I think what you're trying to achieve by calculating MI is essentially similar but may be just the wrong carriage for your charge.
Not knowing the details of your scenario, I should think that you may not even need any labeled data at all, except if you're interested in the labels themselves. Just cluster your data once, let the user pick an item interesting to him/her from the central members of all clusters and suggest other items from the selected clusters as perhaps being interesting as well. Also suggest some random instances from other clusters here and there, so that if the user selects one of these, you may assume that the corresponding cluster might generally be interesting, too. If there is a contradiction and a user likes some members of a cluster but not some others of the same one, then you try to re-cluster the data into finer-grained groups which discriminate the good from the bad ones. The re-training step could even be avoided by using hierarchical clustering from the start and traveling down the cluster hierarchy at every contradiction user input causes.