如何从等值线生成 3D 曲面？

Question

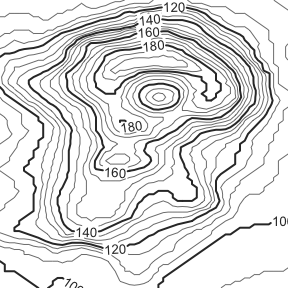
我有一组等值线点（或轮廓点），如下所示：

等值线上的每个点都有其各自的 X、Y 和 Z 坐标。由于它们是等值线，这意味着每个点将具有唯一的 XY 对，但同一条线上的点将具有相同的 Z 坐标。

现在，是否有任何算法或任何软件包（C# 或 C++ 或 MATLAB 语言）可以用来将等值线点插值到完整的 3-D 表面中？

P/S：我不仅对最终输出感兴趣，我对获取插值表面数据感兴趣，以便我可以自己绘制表面。

编辑：C++ 解决方案也受到欢迎。

Answer 1

在 MATLAB 中，您可以使用函数 griddata 或 TriScatteredInterp 类 (注意：从 R2013a 开始 scatteredInterpolant 是推荐的替代方案）。这两种方法都允许您将规则间隔的数据曲面拟合到一组非均匀间隔的点（尽管在较新的 MATLAB 版本中似乎不再建议使用 griddata）。下面介绍了如何使用它们：

• griddata:

  [XI,YI,ZI] = griddata(x,y,z,XI,YI)
  

  其中x,y,z分别表示每个点（在本例中为等高线上的点）的笛卡尔坐标向量。行向量 XI 和列向量 YI 是笛卡尔坐标，griddata 在该坐标处对拟合的值 ZI 进行插值表面。矩阵 XI,YI 返回的新值与将 XI,YI 传递到 meshgrid 创建统一的点网格。

• TriScatteredInterp 类：

  [XI,YI] = meshgrid(...);
  F = TriScatteredInterp(x(:),y(:),z(:));
  ZI = F(XI,YI);
  

  其中x,y,z再次表示每个点的笛卡尔坐标向量，只是这次我使用了冒号重塑操作 (:) 以确保每个都是一个列向量 ( TriScatteredInterp 所需的格式）。然后使用矩阵 XI,YI 计算插值 F，您必须使用 meshgrid 创建该矩阵。

示例&比较

以下是一些示例代码及其生成的结果图，用于使用上述两种方法从轮廓数据重建表面。轮廓数据是使用 contour 函数：

% First plot:

subplot(2,2,1);
[X,Y,Z] = peaks;  % Create a surface
surf(X,Y,Z);
axis([-3 3 -3 3 -8 9]);
title('Original');

% Second plot:

subplot(2,2,2);
[C,h] = contour(X,Y,Z);  % Create the contours
title('Contour map');

% Format the coordinate data for the contours:

Xc = [];
Yc = [];
Zc = [];
index = 1;
while index < size(C,2)
  Xc = [Xc C(1,(index+1):(index+C(2,index)))];
  Yc = [Yc C(2,(index+1):(index+C(2,index)))];
  Zc = [Zc C(1,index).*ones(1,C(2,index))];
  index = index+1+C(2,index);
end

% Third plot:

subplot(2,2,3);
[XI,YI] = meshgrid(linspace(-3,3,21));  % Generate a uniform grid
ZI = griddata(Xc,Yc,Zc,XI,YI);          % Interpolate surface
surf(XI,YI,ZI);
axis([-3 3 -3 3 -8 9]);
title('GRIDDATA reconstruction');

% Fourth plot:

subplot(2,2,4);
F = TriScatteredInterp(Xc(:),Yc(:),Zc(:));  % Generate interpolant
ZIF = F(XI,YI);                             % Evaluate interpolant
surf(XI,YI,ZIF);
axis([-3 3 -3 3 -8 9]);
title('TriScatteredInterp reconstruction');

请注意，两个结果之间几乎没有什么区别（至少在这个比例下）。另请注意，由于这些点处轮廓数据的稀疏性，插值曲面在拐角附近有空白区域。

Answer 2

您可以使用 MATLAB Central 文件中的 gridfit 工具交换。我给出的示例之一正是您想要做的，从从等值线获取的点列表开始，我根据数据重建平滑的表面。事实上，我使用的例子取自地形图。

Answer 3

我认为你想要的是所谓的“轮廓缝合”，例如在 this 中讨论的纸

Answer 4

MATLAB 有一个名为 SURF 的内置命令采用 X、Y、Z 的三个数组并绘制曲面。这可能就是您正在寻找的。