查找一个角度与另一个角度是否在 X 度范围内

Question

我需要一种算法来确定一个角度与另一个角度的夹角是否在一定范围内。

我的第一个想法是 (ax < b) && (a+x > b)，但当它必须处理从 -179 到 180 的角度时，它会失败。

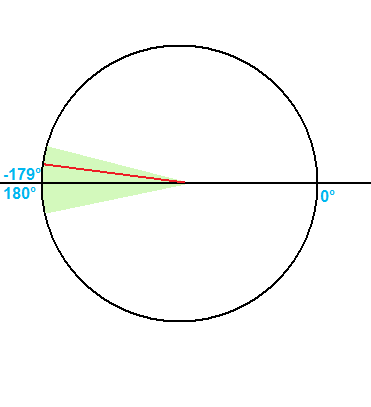
在上图中，角度必须位于负边和正边之间的区域（绿色）。如何确定角度（红线）是否落在该区域内？

Answer 1

尝试这个公式：

360-(|a-b|)%360<x || (|a-b|)%360<x

或者，在 PHP 中：

<?php

$b = 10;
$angle1 = -179;
$angle2 = 180;

$diff = $angle1 - $angle2;
if(abs($diff % 360) <= $b || (360-abs($diff % 360))<=$b) {
  echo "yes";
} else {
  echo "no";
}

?>

Answer 2

正如马塞尔正确指出的那样，负数取模可能存在问题。另外，355度和5度有什么区别？计算结果可能为 350 度，但人们期望的可能是 10 度。我们做出以下假设：

1. 我们希望其他两个角度之间的最小正角度，因此 0 <= diff <= 180;
2. 我们正在以学位为单位工作。如果是弧度，则用 360 代替 2*PI；
3. 角度可以是正值或负值，可以超出范围 -360 < x < 360 其中 x 是输入角度，
4. 输入角度的顺序或差值的方向无关。

输入：角度 a 和 b。所以算法很简单：

1. 将 a 和 b 归一化为 0 <= x 0 <= x 360；
2. 计算两个法线角之间的最短角。

第一步，要将角度转换为所需的范围，有两种可能性：

• x >= 0：Normal = x % 360
• x < 0: 正常 = (-x / 360 + 1) * 360 + x

第二个旨在消除负模运算解释差异上的任何歧义。举一个 x = -400 的例子：

  -x / 360 + 1
= -(-400) / 360 + 1
= 400 / 360 + 1
= 1 + 1
= 2

那么

normal = 2 * 360 + (-400)
       = 320

对于输入 10 和 -400，法向角度是 10 和 320。

现在我们计算它们之间的最短角度。作为健全性检查，这两个角度的总和必须为 360。在本例中，可能性为 50 和 310（画出来，您就会看到这一点）。要解决这些问题：

normal1 = min(normal(a), normal(b))
normal2 = max(normal(a), normal(b))
angle1 = normal2 - normal1
angle2 = 360 + normal1 - normal2

对于我们的示例：

normal1 = min(320, 10) = 10
normal2 = max(320, 10) = 320
angle1 = normal2 - normal1 = 320 - 10 = 310
angle2 = 360 + normal1 - normal2 = 360 + 10 - 320 = 50

您将注意到 normal1 + normal2 = 360 （如果您愿意，您甚至可以证明情况就是如此）。

最后：

diff = min(normal1, normal2)

在我们的例子中是 50。

Answer 3

您还可以使用点积：

cos(a)*cos(b) + sin(a)*sin(b) >= cos(x)

Answer 4

对于半径为 1 的情况，直线端点之间的距离为 2sin((ab/2)。因此丢弃 2，因为您只对比较感兴趣，并将 sin(x/2) 与 sin((ab)/ 2). 三角函数负责所有的包装。

Answer 5

C++实现：

float diff = fabsf(angle1 - angle2);
bool isInRange = fmodf(diff, 360.0f) <= ANGLE_RANGE ||
                 360.0f - fmodf(diff, 360.0f) <= ANGLE_RANGE;