计算至“无限” C# 中的二进制精度
到目前为止,法布里斯·贝拉德 (Fabrice Bellard) 的基数为 2 的方程似乎是可行的
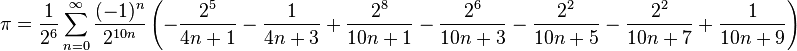
讽刺的是这将需要 BigReal 类型;我们有 .Net 的这个吗? .Net 4.0 有 BigInteger。
有人有 Haskell 版本吗?
So far it looks like Fabrice Bellard's base 2 equation is the way to go
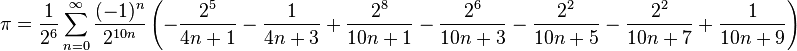
Ironically this will require a BigReal type; do we have this for .Net? .Net 4.0 has BigInteger.
Anyone have a Haskell version?
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(4)
由于您需要 Haskell 版本,这里有一篇 Jerzy 的论文 Karczmarczuk,被称为“世界上最不可靠的计算 π 的技术”:
它并没有真正以有效或非常实用的方式解决问题,但很有趣,并通过惰性无限精度算术展示了一些问题。
然后还有 Jeremy Gibbons 的这篇论文 。
Since you're asking for a Haskell version, here is a paper by Jerzy Karczmarczuk, called "The Most Unreliable Technique in the World to compute π":
It doesn't really solve the problem in an efficient or very practical way, but is entertaining and shows some of the problems with lazy infinite precision arithmetic.
Then there's also this paper by Jeremy Gibbons.
到目前为止,我最喜欢的 pi 的 Haskell spigot 来自 Jeremy Gibbons:
证明该实现合理的数学背景可以在以下位置找到:
Pi 数字的插销算法
By far my favorite Haskell spigot for pi comes from Jeremy Gibbons:
The mathematical background that justifies that implementation can be found in:
A Spigot Algorithm for the Digits of Pi
维基百科详细介绍了许多获取 pi 数值近似值的方法此处。他们还提供了一些示例伪代码
编辑:如果您对此类数学问题感兴趣,但没有任何相关的现实世界问题需要解决(恕我直言,这绝对是一个好的态度),您可以访问 Euler 项目页面
Wikipedia details a lot of ways to get numerical approximations of pi here. They also give some sample pseudo-code
Edit : If you're interested in this kind of mathematical problems without having any related real-world problem to solve (which is definitely a good attitude to have, IMHO), you could visit the Euler Project page
在基于 DLR 的动态语言中,存在处理大有理数的可能性(例如 IronPython)。或者,您可以通过 P/Invoke 使用大实数的任何可移植 C/C++ 实现。
There exists such possibility to process big rational numbers in DLR-based dynamic languages (e.g. IronPython). Or you can use any portable C/C++ implementation of big real numbers through P/Invoke.