解决8字谜题的有效方法是什么？

Question

8 拼图是一块有 9 个位置的方板，由 8 个编号的图块和一个间隙填充。在任何时候，与间隙相邻的图块都可以移动到间隙中，从而创建新的间隙位置。换句话说，间隙可以与相邻（水平和垂直）的图块交换。游戏的目标是从任意配置的图块开始，然后移动它们以使编号的图块按升序排列，或者沿着棋盘的周边运行，或者从左到右排序，其中 1 在左上角-手的位置。

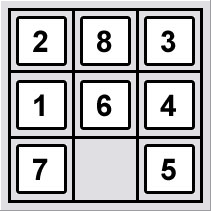
我想知道什么方法可以有效解决这个问题？

Answer 1

我将尝试重写之前的答案，并详细说明为什么它是最佳的。

直接取自 wikipedia 的 A* 算法是

            function A*(start,goal)
                    closedset := the empty set                 // The set of nodes already evaluated.     
                    openset := set containing the initial node // The set of tentative nodes to be evaluated.
                    came_from := the empty map                 // The map of navigated nodes.
                    g_score[start] := 0                        // Distance from start along optimal path.
            h_score[start] := heuristic_estimate_of_distance(start, goal)
                    f_score[start] := h_score[start]           // Estimated total distance from start to goal through y.
                    while openset is not empty
                    x := the node in openset having the lowest f_score[] value
                    if x = goal
            return reconstruct_path(came_from, came_from[goal])
                    remove x from openset
                    add x to closedset
            foreach y in neighbor_nodes(x)
                    if y in closedset
                    continue
            tentative_g_score := g_score[x] + dist_between(x,y)

                    if y not in openset
                    add y to openset
                    tentative_is_better := true
                    elseif tentative_g_score < g_score[y]
                    tentative_is_better := true
                    else
                    tentative_is_better := false
                    if tentative_is_better = true
                    came_from[y] := x
                    g_score[y] := tentative_g_score
            h_score[y] := heuristic_estimate_of_distance(y, goal)
                    f_score[y] := g_score[y] + h_score[y]
                    return failure

            function reconstruct_path(came_from, current_node)
                    if came_from[current_node] is set
                    p = reconstruct_path(came_from, came_from[current_node])
            return (p + current_node)
                    else
                    return current_node

所以让我在这里填写所有详细信息。

heuristic_estimate_of_distance 是函数 Σ d(x_i)，其中 d(.) 是每个方格 x_i 与其目标状态的曼哈顿距离。

因此，该设置

            1 2 3
            4 7 6
            8 5 

的 heuristic_estimate_of_distance 为 1+2+1=4，因为 8,5 中的每一个距离其目标位置 1，d(.)=1，7 距离其目标 2状态 d(7)=2。

A* 搜索的节点集被定义为起始位置，后跟所有可能的合法位置。也就是说，起始位置 x 如上所述：

            x =
            1 2 3
            4 7 6
            8 5 

然后函数 neighbor_nodes(x) 产生 2 个可能的合法移动：

            1 2 3
            4 7 
            8 5 6

            or

            1 2 3
            4 7 6
            8   5

函数 dist_ Between(x,y) ) 定义为从状态 x 转换到 y 所发生的方块移动次数。出于算法的目的，在 A* 中这通常等于 1。

closeset 和 openset 都是 A* 算法特有的，可以使用标准数据结构（我相信优先级队列）来实现。 came_from 是一个使用的数据结构
使用函数reconstruct_path重建找到的解决方案，其详细信息可以在维基百科上找到。如果您不想记住解决方案，则无需实施此解决方案。

最后，我将讨论最优性问题。考虑 A* 维基百科文章的摘录：

“如果启发式函数 h 是可接受的，这意味着它永远不会高估达到目标的实际最小成本，那么如果我们不使用封闭式，A* 本身就是可接受的（或最佳的）如果使用闭集，则 h 也必须是单调的（或一致的），A* 才是最优的，这意味着对于任何一对相邻节点 x 和 y，其中 d(x,y) 表示 的长度。他们之间的边缘，我们必须有：
h(x) <= d(x,y) +h(y)"

因此足以表明我们的启发式是可接受的且单调的。对于前者（可接受性），请注意，给定任何配置，我们的启发式（所有启发式的总和）距离）估计每个方格不仅仅受到合法移动的约束，并且可以自由地向其目标位置移动，这显然是一个乐观的估计，因此我们的启发式是可接受的（或者它永远不会高估，因为到达目标位置总是需要 < em>至少与启发式估计一样多的动作。）

用文字表述的单调性要求是：
“任何节点的启发式成本（到目标状态的估计距离）必须小于或等于转换到任何相邻节点的成本加上该节点的启发式成本。”

它主要是为了防止出现负循环的可能性，即转换到不相关的节点可能会比实际进行转换的成本减少到目标节点的距离，这表明启发式很差。

在我们的例子中，显示单调性非常简单。根据我们对 d 的定义，任何相邻节点 x,y 都具有 d(x,y)=1。因此我们需要证明

h(x) <= h(y) + 1

相当于

h(x) - h(y) <= 1

相当于

Σ d(x_i) - Σ d(y_i) <= 1

相当于

Σ d(x_i) - d(y_i) <= 1

根据 neighbor_nodes(x) 的定义，我们知道两个邻居节点 x,y 最多可以有一个方格的位置不同，这意味着在我们的总和中，项

d(x< sub>i) - d(y_i) = 0

对于除 1 之外的所有 i 值。不失一般性地说，i=k 是这样。此外，我们知道，对于 i=k，节点最多移动了一处，因此它到
目标状态最多只能比前一个状态多 1，因此：

Σ d(x_i) - d(y_i) = d(x_k ) - d(y_k) <= 1

显示单调性。这显示了需要显示的内容，从而证明该算法将是最优的（以大 O 表示法或渐近方式）。

请注意，我已经在大 O 表示法方面展示了最优性，但仍然有很多空间调整启发式。您可以对其添加额外的扭曲，以便更接近地估计到目标状态的实际距离，但是您必须确保启发式始终是< em>低估否则你就会失去最优性！

很久以后

编辑这篇文章（很久）之后，我意识到我写它的方式有点混淆了这个算法的最优性的含义。

我在这里试图理解的最优性有两个不同的含义：

1）算法产生最优解决方案，即给定客观标准的最佳可能解决方案。

2) 该算法使用相同的启发式扩展了所有可能算法的最少状态节点数。

理解为什么需要启发式的可接纳性和单调性来获得 1) 的最简单方法是将 A* 视为 Dijkstra 最短路径算法在图上的应用，其中边权重由迄今为止移动的节点距离加上启发式给出距离。如果没有这两个属性，我们就会在图中出现负边，从而可能出现负循环，并且 Dijkstra 的最短路径算法将不再返回正确答案！ （构造一个简单的例子来说服自己。）

2）实际上很难理解。为了充分理解这句话的意思，这个说法有很多量词，比如在谈论其他算法时，指的是像A*这样的类似算法，它扩展节点并在没有先验的情况下进行搜索显然，我们可以构造一个简单的反例，例如神谕或精灵在每一步都告诉您答案。要深入理解此声明，我强烈建议阅读维基百科<历史部分的最后一段/a> 以及查看该仔细陈述的句子中的所有引文和脚注。

我希望这能消除潜在读者中剩余的困惑。

Answer 2

您可以使用基于数字位置的启发式，即每个字母与其目标状态的所有距离的总和越高，启发式值就越高。然后您可以实现 A* 搜索，这可以被证明是时间和空间复杂度方面的最佳搜索（假设启发式是单调且可接受的。） http://en.wikipedia.org/wiki/A*_search_algorithm

Answer 3

由于OP无法发布图片，这就是他所说的：

就解决而言这个难题，去看看迭代加深深度优先搜索算法，正如此页面与 8-puzzle 问题相关的内容。

Answer 4

甜甜圈搞定了！考虑到这个难题的搜索空间相对有限，IDDFS 就能解决这个问题。因此回答OP的问题会很有效。它会找到最优解，但不一定是最优复杂度。

实现 IDDFS 将是这个问题中更复杂的部分，我只是想建议一种简单的方法来管理棋盘、游戏规则等。这特别解决了一种获取可解谜题的初始状态的方法。问题注释中暗示，并非所有 9 个点的随机分配（将空槽视为特殊图块）都会产生可解决的难题。这是数学奇偶性的问题......所以，这里有一个对游戏进行建模的建议：

列出代表游戏有效“移动”的所有 3x3 排列矩阵。
这样的列表是 3x3 的子集（全零和两个 1）。每个矩阵都有一个 ID，这对于在 IDDFS 搜索树中跟踪移动非常方便。矩阵的替代方案是交换瓦片位置编号的二元组，这可能会导致更快的实现。

这样的矩阵可用于创建初始拼图状态，从“获胜”状态开始，并运行随机选择的任意数量的排列。除了确保初始状态是可解的之外，这种方法还提供了可以解决给定谜题的指示性移动次数。

现在让我们实现 IDDFS 算法并[笑话]返回 A+ 的作业[/笑话]...

Answer 5

这是经典最短路径算法的一个例子。您可以在此处和此处。

简而言之，将拼图的所有可能状态视为某个图中的顶点。每次移动都会改变状态 - 因此，每个有效的移动都代表图形的一条边。由于移动没有任何成本，您可能会认为每次移动的成本为 1。以下类似 C++ 的伪代码适用于解决此问题：

{
int[][] field = new int[3][3];
//  fill the input here
map<string, int> path;
queue<string> q;
put(field, 0); // we can get to the starting position in 0 turns
while (!q.empty()) {
    string v = q.poll();
    int[][] take = decode(v); 
    int time = path.get(v);
    if (isFinalPosition(take)) {
        return time;
    }
    for each valid move from take to int[][] newPosition {
        put(newPosition, time + 1);
    }
}
// no path
return -1;
}

void isFinalPosition(int[][] q) {
    return encode(q) == "123456780"; // 0 represents empty space
}
void put(int[][] position, int time) {
    string s = encode(newPosition);
    if (!path.contains(s)) {
        path.put(s, time);
    }
}

string encode(int[][] field) {
    string s = "";
    for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) s += field[i][j];
    return s;
}

int[][] decode(string s) {
    int[][] ans = new int[3][3];
    for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) field[i][j] = s[i * 3 + j];
    return ans;
}

Answer 6

请参阅此链接，了解我的并行加深迭代深入搜索15个难题的解决方案，它是 8 拼图的 4x4 老大哥。