组合计数谜题:掷 20 个 8 面骰子,得到至少 5 个相同值的骰子的概率是多少
假设在一场游戏中,一个人掷 20 个 8 面骰子,总共有 8^20 种可能的结果。 为了计算特定事件发生的概率,我们将该事件发生的方式数除以 8^20。
我们可以计算出恰好获得 5 个骰子的值 3 的方法数。(20 选择 5)给出了 3 的阶数。7^15 给出了我们在 15 次掷骰中无法获得值 3 的方法数。
number of ways to get exactly 5, 3's = (20 choose 5)*7^15.
答案也可以被视为有多少种方法可以重新排列字符串 3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0 ,0,0(20 选择 5)乘以零的值总数(假设 7 个合法值)7^15(这是正确的)。
问题 1:如何计算获得恰好 5 个相同值的骰子的方法数(即,对于所有骰子值)。 注意:如果我只是天真地使用上面的第一个答案并乘以 bt 8,我会得到大量的重复计算?
我知道我可以解决每种情况 (5 1's)、(5, 2's)、(5, 3's)、... (5's, 8) 将它们相加(更简单地说 8*(5 1's) )。 然后减去重叠数的总和 (5 1's) 和 (5 2's)、(5 1's) 和 (5 3's)... (5 1's) 和 (5, 2's) 以及 ... 和 (5, 8's)但这看起来非常混乱。 我会以一种扩展到大量样本和大量类的方式对此进行概括。
如何计算获得至少 5 个相同值骰子的方法数?
所以 111110000000000000000 或 11110100000000000002 或 11111100000001110000 或 11011211222222223333,但不是 00001111222233334444 或 00051 1512252363347744.
我正在寻找解释数学或指向支持此功能的库(尤其是 python 模块)的答案。 细节和例子加分。
Assume a game in which one rolls 20, 8-sided die, for a total number of 8^20 possible outcomes. To calculate the probability of a particular event occurring, we divide the number of ways that event can occur by 8^20.
One can calculate the number of ways to get exactly 5 dice of the value 3. (20 choose 5) gives us the number of orders of 3. 7^15 gives us the number of ways we can not get the value 3 for 15 rolls.
number of ways to get exactly 5, 3's = (20 choose 5)*7^15.
The answer can also be viewed as how many ways can I rearrange the string 3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 (20 choose 5) times the total number of values we the zero's (assuming 7 legal values) 7^15 (is this correct).
Question 1: How can I calculate the number of ways to get exactly 5 dice of the same value(That is, for all die values).
Note: if I just naively use my first answer above and multiply bt 8, I get an enormous amount of double counting?I understand that I could solve for each of the cases (5 1's), (5, 2's), (5, 3's), ... (5's, 8) sum them (more simply 8*(5 1's) ). Then subtract the sum of number of overlaps (5 1's) and (5 2's), (5 1's) and (5 3's)... (5 1's) and (5, 2's) and ... and (5, 8's) but this seems exceedingly messy. I would a generalization of this in a way that scales up to large numbers of samples and large numbers of classes.
How can I calculate the number of ways to get at least 5 dice of the same value?
So 111110000000000000000 or 11110100000000000002 or 11111100000001110000 or 11011211222222223333, but not 00001111222233334444 or 000511512252363347744.
I'm looking for answers which either explain the math or point to a library which supports this (esp python modules). Extra points for detail and examples.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(7)
我建议您花一点时间编写蒙特卡罗模拟,并让它运行,同时您手工计算数学。 希望蒙特卡洛模拟能够在您完成数学计算之前收敛,并且您将能够检查您的解决方案。
稍微快一点的选择可能涉及为数学问题创建一个 SO 克隆。
I suggest that you spend a little bit of time writing up a Monte Carlo simulation and let it run while you work out the math by hand. Hopefully the Monte Carlo simulation will converge before you're finished with the math and you'll be able to check your solution.
A slightly faster option might involve creating a SO clone for math questions.
重复计算可以通过使用包含/排除原则来解决,
我怀疑它出来了至:
等等。 这并不能直接解决“超过 5 个相同的”问题,就好像您只是将其应用到 5,6,7..20 的结果相加; 你可能会过多地计算有 10 个 1 和 5 个 8 的情况。
您可能可以再次应用包含排除来得出第二个答案; 所以,P(至少 5 个)=P(一组 20 个)+ ... + (P(一组 15 个) - 7*P(一组 5 个骰子,共 5 个)) + ((P(一组) 14) - 7*P(6 中的一组 5) - 7*P(6 中的一组 6)) 证明其源代码本身更加困难。
Double counting can be solved by use of the Inclusion/Exclusion Principle
I suspect it comes out to:
And so on. This doesn't solve the problem directly of 'more then 5 of the same', as if you simply summed the results of this applied to 5,6,7..20; you would over count the cases where you have, say, 10 1's and 5 8's.
You could probably apply inclusion exclusion again to come up with that second answer; so, P(of at least 5)=P(one set of 20)+ ... + (P(one set of 15) - 7*P(set of 5 from 5 dice)) + ((P(one set of 14) - 7*P(one set of 5 from 6) - 7*P(one set of 6 from 6)). Coming up with the source code for that is proving itself more difficult.
i 个 s 面骰子之和的精确概率分布 Fs,i 可以通过单骰子概率分布与其自身的重复卷积来计算。
其中 对于所有
对于所有  ,否则为 0。
,否则为 0。
http://en.wikipedia.org/wiki/Dice
The exact probability distribution Fs,i of a sum of i s-sided dice can be calculated as the repeated convolution of the single-die probability distribution with itself.
where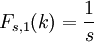 for all
for all  and 0 otherwise.
and 0 otherwise.
http://en.wikipedia.org/wiki/Dice
如果你必须概括它(得到精确的公式),这个问题真的很难。
但无论如何,让我解释一下算法。
如果你想知道
您必须重新表述之前的问题,如
,我们将函数 F(20,8,5)(5 个骰子,所有值)称为第一个答案,将 F(20,8,5,3)(5 个骰子,值 3)称为第二个答案。
我们有 F(20,8,5) = F(20,8,5,3) * 8 + (多个值重复 5 次时的事件)
所以如果我们可以得到 F (20,8,5,3) 应该很简单不是吗?
好吧...没那么多...
首先,让我们定义一些变量:
X1,X2,X3...,Xi ,其中 Xi=我们获得骰子 i 的次数
那么:
,P(语句) 是编写概率的标准方法。
我们继续:
递归地:
那么... F(5,5,5,4) 是在 5 次投掷中获得 5 个值为 4 的骰子的方法数,例如没有其他骰子重复 5 次。 总共 5^5 种方法中,只有 1 种方法。 那么概率就是 1/5^5。
F(5,5,5) 是在 5 次掷骰中获得 5 个任意值(共 5 个值)的骰子的方法数。 显然是5。那么概率就是5/5^5 = 1/5^4。
F(10,6,5,2)是在没有其他骰子重复5次的情况下,在10次投掷中获得5个值为2的骰子的方法数。
F(10,6,5,2) = (1-F(5,5,5)/5^5) * 6^10 = (1-1/5^4) * 6^10
嗯...我认为它在某些部分可能不正确,但无论如何,你明白了。 我希望我能让算法易于理解。
编辑:
我做了一些检查,我意识到当你得到多个值重复恰好 5 次时,你必须添加一些情况。 你没有时间解决那部分......
This problem is really hard if you have to generalize it (get the exact formula).
But anyways, let me explain the algorithm.
If you want to know
you have to rephrase your previous problem, as
For simplicity's sake, let's call function F(20,8,5) (5 dice, all values) the first answer, and F(20,8,5,3) (5 dice, value 3) the second.
We have that F(20,8,5) = F(20,8,5,3) * 8 + (events when more than one value is repeated 5 times)
So if we can get F(20,8,5,3) it should be pretty simple isn't it?
Well...not so much...
First, let us define some variables:
X1,X2,X3...,Xi , where Xi=number of times we get the dice i
Then:
, P(statement) being the standard way to write a probability.
we continue:
recursively:
Well then... F(5,5,5,4) is the number of ways to get 5 dices of value 4 in 5 rolls, such as no other dice repeats 5 times. There is only 1 way, out of a total 5^5. The probability is then 1/5^5.
F(5,5,5) is the number of ways to get 5 dices of any value (out of 5 values) in 5 rolls. It's obviously 5. The probability is then 5/5^5 = 1/5^4.
F(10,6,5,2) is the number of ways to get 5 dices of value 2 in 10 rolls, such as no other dice repeats 5 times.
F(10,6,5,2) = (1-F(5,5,5)/5^5) * 6^10 = (1-1/5^4) * 6^10
Well... I think it may be incorrect at some part, but anyway, you get the idea. I hope I could make the algorithm understandable.
edit:
I did some checks, and I realized you have to add some cases when you get more than one value repeated exactly 5 times. Don't have time to solve that part thou...
这就是我的想法……
如果你只有 5 个骰子,你就只有 8 种方法来得到你想要的东西。
对于这八种方式中的每一种,其他 15 个骰子的所有可能组合都有效。
所以 - 我认为答案是: (8 * 815) / 820
(至少 5 的答案是相同的。)
Here is what I am thinking...
If you just had 5 dice, you would only have eight ways to get what you want.
For each of those eight ways, all possible combinations of the other 15 dice work.
So - I think the answer is: (8 * 815) / 820
(The answer for at least 5 the same.)
我相信你可以使用 n 个事件中 x 次出现的公式为:
P = 概率^n * (n!/((n - x)!x!))
所以最终结果将是 0 的结果之和到 n.
我真的没有看到任何简单的方法可以将其合并为一个不会那么混乱的步骤。 通过这种方式,您也可以在代码中拼写出公式。 不过,您可能必须编写自己的阶乘方法。
I believe you can use the formula of x occurrences in n events as:
P = probability^n * (n!/((n - x)!x!))
So the final result is going to be the sum of results from 0 to n.
I don't really see any easy way to combine it into one step that would be less messy. With this way you have the formula spelled out in the code as well. You may have to write your own factorial method though.
递归解法:
Recursive solution: