计算“饼图段”面积的边界点 和“子区域”

Question

背景：

我最近正在使用 GDI+ 绘制一个“光盘”，显示 360 度的全面颜色变化。 （我挖了一些HSL到RGB的代码来循环HSL(1,1,1) -> HSL(360,1,1)）

关于光盘，我首先使用上面的方法画了一个完整的实心圆，然后中心上的第二个灰色圆圈给出以下

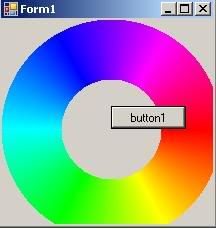
所以这一切都很好..但我意识到 GDI+ 使我们免受通过 FillPie 方法进行的许多棘手的匹配。 此外，FillPie 要求您提供饼图的边界矩形，而不是半径长度。 它还执行完整的段填充，并且不允许您仅指定该段的一部分。

问题：

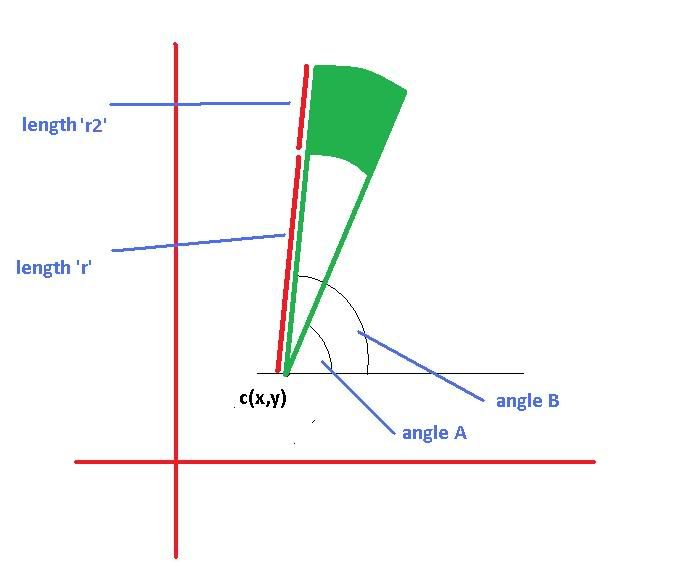
任何人都可以向我指出一些数学函数的方向，或者对我需要什么论坛来计算面积和面积给出任何解释吗？ 给出以下“绿色填充区域”的绘图点：

Point `c` - an x,y co-ordinate
Angle `A` - an angle from horizontal
Angle `B  - an angle from horizontal where `B` - `A` == the sweep angle
Length `r` - a distance from `c`
Length `r2` - a distance from `c` where `r2` - `r` == the `height` of the segment to be filled.

数学源的链接很好但我已经快速谷歌& 看看 Wolfram Math 可以找到我正在寻找的东西。 另外，如果有某种方法可以生成可以作为 Point[] 传递给 Graphics.FillPolygon 的边界 (x,y) co-or 序列，那也很酷。

Answer 1

该面积是外圆盘部分和内圆盘部分的差。 圆盘部分的面积与扫角成正比：

area = (b-a)*((r+r2)^2-r^2)/2

a 和 b 必须以弧度表示。
对于ba = 2*Pi，area = Pi*(r+r2)^2 - Pi*r^2是外盘和内盘面积之差。

在内/外圆上生成点。

x = cx + r * cos(t)     /     x = cx + (r+r2) * cos(t)
y = cy + r * sin(t)     /     y = cy + (r+r2) * sin(t)

您可以使用其中 t 从 a 到 b 变化的方式

Answer 2

希望这可以帮助。 第二部分提供了计算圆扇形面积的方法

http://www.wikihow.com/Calculate-the-Area-of-a-Circle

Answer 3

圆弧的面积就是圆弧的角度（以弧度为单位）乘以半径。 所以绿色圆圈的面积显然是：

(B-A) * r2

Answer 4

您需要画线（此伪代码）：

for aa from A to B
  set color to required color // you could use aa in an equation with HSL to get something like your sample
  x1=r*cos(aa)+x
  y1=r*sin(aa)+y
  x2=r1*cos(aa)+x
  y2=r1*sin(aa)+y
  draw line between (x1,y1) and (x2,y2)

对于足够小的角度增量和足够小的半径，这应该没问题。

您要寻找的点是每个角度 aa 的 (x1,y1) 和 (x2,y2)