当前位置： 文江博客 话题详情

找到两个给定节点之间的路径？

发布于 2024-07-16 06:35:08 字数 2220 浏览 10 评论 0 原文

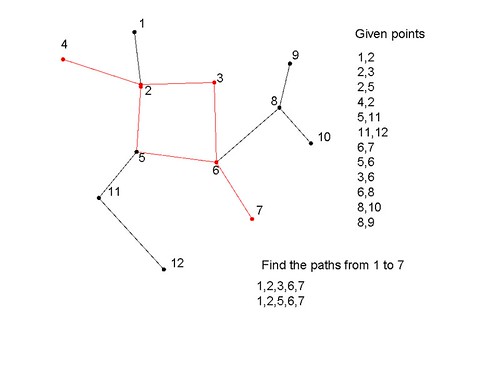
假设我有以下方式连接的节点，如何获得给定点之间存在的路径数量以及路径详细信息？

1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9

求从1到7的路径：

答案： 找到 2 个路径，它们是

1,2,3,6,7
1,2,5,6,7

alt text

找到的实现 这里 很好，我将使用相同的

这里是上面链接中 python 的片段

# a sample graph
graph = {'A': ['B', 'C','E'],
             'B': ['A','C', 'D'],
             'C': ['D'],
             'D': ['C'],
             'E': ['F','D'],
             'F': ['C']}

class MyQUEUE: # just an implementation of a queue

    def __init__(self):
        self.holder = []

    def enqueue(self,val):
        self.holder.append(val)

    def dequeue(self):
        val = None
        try:
            val = self.holder[0]
            if len(self.holder) == 1:
                self.holder = []
            else:
                self.holder = self.holder[1:]   
        except:
            pass

        return val  

    def IsEmpty(self):
        result = False
        if len(self.holder) == 0:
            result = True
        return result


path_queue = MyQUEUE() # now we make a queue


def BFS(graph,start,end,q):

    temp_path = [start]

    q.enqueue(temp_path)

    while q.IsEmpty() == False:
        tmp_path = q.dequeue()
        last_node = tmp_path[len(tmp_path)-1]
        print tmp_path
        if last_node == end:
            print "VALID_PATH : ",tmp_path
        for link_node in graph[last_node]:
            if link_node not in tmp_path:
                #new_path = []
                new_path = tmp_path + [link_node]
                q.enqueue(new_path)

BFS(graph,"A","D",path_queue)

-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH :  ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH :  ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH :  ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH :  ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH :  ['A', 'E', 'F', 'C', 'D']
原文

Say I have nodes connected in the below fashion, how do I arrive at the number of paths that exist between given points, and path details?

1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9

Find the paths from 1 to 7:

Answer:
2 paths found and they are 

1,2,3,6,7
1,2,5,6,7

alt text

implementation found here is nice I am going to use the same

Here is the snippet from the above link in python

# a sample graph
graph = {'A': ['B', 'C','E'],
             'B': ['A','C', 'D'],
             'C': ['D'],
             'D': ['C'],
             'E': ['F','D'],
             'F': ['C']}

class MyQUEUE: # just an implementation of a queue

    def __init__(self):
        self.holder = []

    def enqueue(self,val):
        self.holder.append(val)

    def dequeue(self):
        val = None
        try:
            val = self.holder[0]
            if len(self.holder) == 1:
                self.holder = []
            else:
                self.holder = self.holder[1:]   
        except:
            pass

        return val  

    def IsEmpty(self):
        result = False
        if len(self.holder) == 0:
            result = True
        return result


path_queue = MyQUEUE() # now we make a queue


def BFS(graph,start,end,q):

    temp_path = [start]

    q.enqueue(temp_path)

    while q.IsEmpty() == False:
        tmp_path = q.dequeue()
        last_node = tmp_path[len(tmp_path)-1]
        print tmp_path
        if last_node == end:
            print "VALID_PATH : ",tmp_path
        for link_node in graph[last_node]:
            if link_node not in tmp_path:
                #new_path = []
                new_path = tmp_path + [link_node]
                q.enqueue(new_path)

BFS(graph,"A","D",path_queue)

-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH :  ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH :  ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH :  ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH :  ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH :  ['A', 'E', 'F', 'C', 'D']

如果你对这篇内容有疑问，欢迎到本站社区发帖提问 参与讨论，获取更多帮助，或者扫码二维码加入 Web 技术交流群。

扫码二维码加入Web技术交流群

发布评论

需要 登录 才能够评论， 你可以免费 注册 一个本站的账号。

评论（8）

多像笑话 2024-07-23 06:35:08

广度优先搜索遍历一个图，实际上找到从起始节点开始的所有路径。 然而，BFS 通常不会保留所有路径。 相反，它更新前驱函数 π 以保存最短路径。 您可以轻松修改算法，以便 π(n) 不仅存储一个 前驱，还存储可能的前驱列表。

然后所有可能的路径都被编码在这个函数中，通过递归遍历 π 就可以得到所有可能的路径组合。

Cormen 等人在算法简介中可以找到使用这种表示法的一个很好的伪代码，并且随后在许多大学关于该主题的脚本中使用。 通过 Google 搜索“BFS 伪代码前身 π”，Stack Exchange 上的这一搜索结果被连根拔起。

Breadth-first search traverses a graph and in fact finds all paths from a starting node. Usually, BFS doesn't keep all paths, however. Instead, it updates a prededecessor function π to save the shortest path. You can easily modify the algorithm so that π(n) doesn't only store one predecessor but a list of possible predecessors.

Then all possible paths are encoded in this function, and by traversing π recursively you get all possible path combinations.

One good pseudocode which uses this notation can be found in Introduction to Algorithms by Cormen et al. and has subsequently been used in many University scripts on the subject. A Google search for “BFS pseudocode predecessor π” uproots this hit on Stack Exchange.

回复 原文
玉环 2024-07-23 06:35:08

对于那些不是 PYTHON 专家的人，C++ 中的相同代码

//@Author :Ritesh Kumar Gupta
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int> >GRAPH(100);
inline void print_path(vector<int>path)
{
    cout<<"[ ";
    for(int i=0;i<path.size();++i)
    {
        cout<<path[i]<<" ";
    }
    cout<<"]"<<endl;
}
bool isadjacency_node_not_present_in_current_path(int node,vector<int>path)
{
    for(int i=0;i<path.size();++i)
    {
        if(path[i]==node)
        return false;
    }
    return true;
}
int findpaths(int source ,int target ,int totalnode,int totaledge )
{
    vector<int>path;
    path.push_back(source);
    queue<vector<int> >q;
    q.push(path);

    while(!q.empty())
    {
        path=q.front();
        q.pop();

        int last_nodeof_path=path[path.size()-1];
        if(last_nodeof_path==target)
        {
            cout<<"The Required path is:: ";
            print_path(path);
        }
        else
        {
            print_path(path);
        }

        for(int i=0;i<GRAPH[last_nodeof_path].size();++i)
        {
            if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path))
            {

                vector<int>new_path(path.begin(),path.end());
                new_path.push_back(GRAPH[last_nodeof_path][i]);
                q.push(new_path);
            }
        }




    }
    return 1;
}
int main()
{
    //freopen("out.txt","w",stdout);
    int T,N,M,u,v,source,target;
    scanf("%d",&T);
    while(T--)
    {
        printf("Enter Total Nodes & Total Edges\n");
        scanf("%d%d",&N,&M);
        for(int i=1;i<=M;++i)
        {
            scanf("%d%d",&u,&v);
            GRAPH[u].push_back(v);
        }
        printf("(Source, target)\n");
        scanf("%d%d",&source,&target);
        findpaths(source,target,N,M);
    }
    //system("pause");
    return 0;
}

/*
Input::
1
6 11
1 2 
1 3
1 5
2 1
2 3
2 4
3 4
4 3
5 6
5 4
6 3
1 4

output:
[ 1 ]
[ 1 2 ]
[ 1 3 ]
[ 1 5 ]
[ 1 2 3 ]
The Required path is:: [ 1 2 4 ]
The Required path is:: [ 1 3 4 ]
[ 1 5 6 ]
The Required path is:: [ 1 5 4 ]
The Required path is:: [ 1 2 3 4 ]
[ 1 2 4 3 ]
[ 1 5 6 3 ]
[ 1 5 4 3 ]
The Required path is:: [ 1 5 6 3 4 ]


*/

For those who are not PYTHON expert ,the same code in C++

//@Author :Ritesh Kumar Gupta
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int> >GRAPH(100);
inline void print_path(vector<int>path)
{
    cout<<"[ ";
    for(int i=0;i<path.size();++i)
    {
        cout<<path[i]<<" ";
    }
    cout<<"]"<<endl;
}
bool isadjacency_node_not_present_in_current_path(int node,vector<int>path)
{
    for(int i=0;i<path.size();++i)
    {
        if(path[i]==node)
        return false;
    }
    return true;
}
int findpaths(int source ,int target ,int totalnode,int totaledge )
{
    vector<int>path;
    path.push_back(source);
    queue<vector<int> >q;
    q.push(path);

    while(!q.empty())
    {
        path=q.front();
        q.pop();

        int last_nodeof_path=path[path.size()-1];
        if(last_nodeof_path==target)
        {
            cout<<"The Required path is:: ";
            print_path(path);
        }
        else
        {
            print_path(path);
        }

        for(int i=0;i<GRAPH[last_nodeof_path].size();++i)
        {
            if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path))
            {

                vector<int>new_path(path.begin(),path.end());
                new_path.push_back(GRAPH[last_nodeof_path][i]);
                q.push(new_path);
            }
        }




    }
    return 1;
}
int main()
{
    //freopen("out.txt","w",stdout);
    int T,N,M,u,v,source,target;
    scanf("%d",&T);
    while(T--)
    {
        printf("Enter Total Nodes & Total Edges\n");
        scanf("%d%d",&N,&M);
        for(int i=1;i<=M;++i)
        {
            scanf("%d%d",&u,&v);
            GRAPH[u].push_back(v);
        }
        printf("(Source, target)\n");
        scanf("%d%d",&source,&target);
        findpaths(source,target,N,M);
    }
    //system("pause");
    return 0;
}

/*
Input::
1
6 11
1 2 
1 3
1 5
2 1
2 3
2 4
3 4
4 3
5 6
5 4
6 3
1 4

output:
[ 1 ]
[ 1 2 ]
[ 1 3 ]
[ 1 5 ]
[ 1 2 3 ]
The Required path is:: [ 1 2 4 ]
The Required path is:: [ 1 3 4 ]
[ 1 5 6 ]
The Required path is:: [ 1 5 4 ]
The Required path is:: [ 1 2 3 4 ]
[ 1 2 4 3 ]
[ 1 5 6 3 ]
[ 1 5 4 3 ]
The Required path is:: [ 1 5 6 3 4 ]


*/
回复 原文
别闹i 2024-07-23 06:35:08

Dijkstra 的算法更多地适用于加权路径，听起来发帖者想要找到所有路径，而不仅仅是最短的路径。

对于此应用程序，我将构建一个图表（您的应用程序听起来不需要定向）并使用您最喜欢的搜索方法。 听起来您想要所有路径，而不仅仅是猜测最短的路径，因此请使用您选择的简单递归算法。

唯一的问题是图是否可以是循环的。

连接：

  • 1, 2
  • 1, 3
  • 2, 3
  • 2, 4

在寻找从 1->4 的路径时，可能会出现 1->4 的循环。 2-> 3-> 1.

在这种情况下，我会在遍历节点时保留一个堆栈。 以下是该图的步骤和生成的堆栈的列表（抱歉格式 - 没有表格选项）：

当前节点（可能的下一个节点减去我们来自的位置）[堆栈]

  1. 1 (2, 3) [1]
  2. 2 (3, 4) [1, 2]
  3. 3 (1) [1, 2, 3]
  4. 1 (2, 3) [1, 2, 3, 1] //错误 - 堆栈上有重复数字 - 检测到循环
  5. 3 () [1, 2, 3] / / 后退到节点 3 并将 1 从堆栈中弹出。 从这里不再有节点可探索
  6. 2 (4) [1, 2] // 后退到节点 2 并将 1 从堆栈中弹出。
  7. 4 () [1, 2, 4] // 找到目标节点 - 记录路径的堆栈。 从这里不再有节点可探索
  8. 2 () [1, 2] //后退到节点 2 并将 4 从堆栈中弹出。 从这里不再有节点可探索
  9. 1 (3) [1] //后退到节点 1 并将 2 从堆栈中弹出。
  10. 3 (2) [1, 3]
  11. 2 (1, 4) [1, 3, 2]
  12. 1 (2, 3) [ 1, 3, 2, 1] //错误 - 堆栈上有重复数字 - 检测到循环
  13. 2 (4) [1, 3, 2] //后退到节点 2 并弹出 1 stack
  14. 4 () [1, 3, 2, 4] 找到目标节点 - 记录堆栈中的一条路径。 从这里不再有节点可探索
  15. 2 () [1, 3, 2] //后退到节点 2 并将 4 从堆栈中弹出。 不再有节点
  16. 3 () [1, 3] // 后退到节点 3 并将 2 从堆栈中弹出。 不再有节点
  17. 1 () [1] // 后退到节点 1 并将 3 从堆栈中弹出。 不再有节点
  18. 完成 2 个记录路径 [1, 2, 4] 和 [1, 3, 2, 4]

Dijkstra's algorithm applies more to weighted paths and it sounds like the poster was wanting to find all paths, not just the shortest.

For this application, I'd build a graph (your application sounds like it wouldn't need to be directed) and use your favorite search method. It sounds like you want all paths, not just a guess at the shortest one, so use a simple recursive algorithm of your choice.

The only problem with this is if the graph can be cyclic.

With the connections:

  • 1, 2
  • 1, 3
  • 2, 3
  • 2, 4

While looking for a path from 1->4, you could have a cycle of 1 -> 2 -> 3 -> 1.

In that case, then I'd keep a stack as traversing the nodes. Here's a list with the steps for that graph and the resulting stack (sorry for the formatting - no table option):

current node (possible next nodes minus where we came from) [stack]

  1. 1 (2, 3) [1]
  2. 2 (3, 4) [1, 2]
  3. 3 (1) [1, 2, 3]
  4. 1 (2, 3) [1, 2, 3, 1] //error - duplicate number on the stack - cycle detected
  5. 3 () [1, 2, 3] // back-stepped to node three and popped 1 off the stack. No more nodes to explore from here
  6. 2 (4) [1, 2] // back-stepped to node 2 and popped 1 off the stack.
  7. 4 () [1, 2, 4] // Target node found - record stack for a path. No more nodes to explore from here
  8. 2 () [1, 2] //back-stepped to node 2 and popped 4 off the stack. No more nodes to explore from here
  9. 1 (3) [1] //back-stepped to node 1 and popped 2 off the stack.
  10. 3 (2) [1, 3]
  11. 2 (1, 4) [1, 3, 2]
  12. 1 (2, 3) [1, 3, 2, 1] //error - duplicate number on the stack - cycle detected
  13. 2 (4) [1, 3, 2] //back-stepped to node 2 and popped 1 off the stack
  14. 4 () [1, 3, 2, 4] Target node found - record stack for a path. No more nodes to explore from here
  15. 2 () [1, 3, 2] //back-stepped to node 2 and popped 4 off the stack. No more nodes
  16. 3 () [1, 3] // back-stepped to node 3 and popped 2 off the stack. No more nodes
  17. 1 () [1] // back-stepped to node 1 and popped 3 off the stack. No more nodes
  18. Done with 2 recorded paths of [1, 2, 4] and [1, 3, 2, 4]
回复 原文
无妨# 2024-07-23 06:35:08

原始代码有点麻烦，如果您想使用 BFS 查找图上两点之间是否存在路径，您可能需要使用 collections.deque。 这是我编写的一个快速解决方案：

注意：如果两个节点之间不存在路径，则此方法可能会无限继续。 我还没有测试所有的情况，YMMV。

from collections import deque

# a sample graph
  graph = {'A': ['B', 'C','E'],
           'B': ['A','C', 'D'],
           'C': ['D'],
           'D': ['C'],
           'E': ['F','D'],
           'F': ['C']}

   def BFS(start, end):
    """ Method to determine if a pair of vertices are connected using BFS

    Args:
      start, end: vertices for the traversal.

    Returns:
      [start, v1, v2, ... end]
    """
    path = []
    q = deque()
    q.append(start)
    while len(q):
      tmp_vertex = q.popleft()
      if tmp_vertex not in path:
        path.append(tmp_vertex)

      if tmp_vertex == end:
        return path

      for vertex in graph[tmp_vertex]:
        if vertex not in path:
          q.append(vertex)

The original code is a bit cumbersome and you might want to use the collections.deque instead if you want to use BFS to find if a path exists between 2 points on the graph. Here is a quick solution I hacked up:

Note: this method might continue infinitely if there exists no path between the two nodes. I haven't tested all cases, YMMV. 

from collections import deque

# a sample graph
  graph = {'A': ['B', 'C','E'],
           'B': ['A','C', 'D'],
           'C': ['D'],
           'D': ['C'],
           'E': ['F','D'],
           'F': ['C']}

   def BFS(start, end):
    """ Method to determine if a pair of vertices are connected using BFS

    Args:
      start, end: vertices for the traversal.

    Returns:
      [start, v1, v2, ... end]
    """
    path = []
    q = deque()
    q.append(start)
    while len(q):
      tmp_vertex = q.popleft()
      if tmp_vertex not in path:
        path.append(tmp_vertex)

      if tmp_vertex == end:
        return path

      for vertex in graph[tmp_vertex]:
        if vertex not in path:
          q.append(vertex)
回复 原文
权谋诡计 2024-07-23 06:35:08

在 Prolog（具体来说，SWI-Prolog）

:- use_module(library(tabling)).

% path(+Graph,?Source,?Target,?Path)
:- table path/4.

path(_,N,N,[N]).
path(G,S,T,[S|Path]) :-
    dif(S,T),
    member(S-I, G), % directed graph
    path(G,I,T,Path).

测试中：

paths :- Graph =
    [ 1- 2  % node 1 and 2 are connected
    , 2- 3 
    , 2- 5 
    , 4- 2 
    , 5-11
    ,11-12
    , 6- 7 
    , 5- 6 
    , 3- 6 
    , 6- 8 
    , 8-10
    , 8- 9
    ],
    findall(Path, path(Graph,1,7,Path), Paths),
    maplist(writeln, Paths).

?- paths.
[1,2,3,6,7]
[1,2,5,6,7]
true.

In Prolog (specifically, SWI-Prolog)

:- use_module(library(tabling)).

% path(+Graph,?Source,?Target,?Path)
:- table path/4.

path(_,N,N,[N]).
path(G,S,T,[S|Path]) :-
    dif(S,T),
    member(S-I, G), % directed graph
    path(G,I,T,Path).

test: 

paths :- Graph =
    [ 1- 2  % node 1 and 2 are connected
    , 2- 3 
    , 2- 5 
    , 4- 2 
    , 5-11
    ,11-12
    , 6- 7 
    , 5- 6 
    , 3- 6 
    , 6- 8 
    , 8-10
    , 8- 9
    ],
    findall(Path, path(Graph,1,7,Path), Paths),
    maplist(writeln, Paths).

?- paths.
[1,2,3,6,7]
[1,2,5,6,7]
true.
回复 原文
没︽人懂的悲伤 2024-07-23 06:35:08

如果需要所有路径，请使用递归。

最好使用邻接列表创建一个函数 f() 来尝试填充当前访问过的顶点列表。 像这样：

void allPaths(vector<int> previous, int current, int destination)
{
    previous.push_back(current);

    if (current == destination)
        //output all elements of previous, and return

    for (int i = 0; i < neighbors[current].size(); i++)
        allPaths(previous, neighbors[current][i], destination);
}

int main()
{
    //...input
    allPaths(vector<int>(), start, end);
}

由于向量是按值传递的（因此在递归过程中进一步进行的任何更改都不是永久性的），因此会枚举所有可能的组合。

您可以通过引用传递前一个向量来提高效率（因此不需要一遍又一遍地复制向量），但您必须确保手动执行 popped_back() 。

还有一件事：如果图表有循环，这将不起作用。
（我假设在这种情况下，您需要找到所有简单路径，然后）在将某些内容添加到前一个向量中之前，首先检查它是否已经存在于其中。

如果您想要所有最短路径，请使用 Konrad 对此算法的建议。

If you want all the paths, use recursion.

Using an adjacency list, preferably, create a function f() that attempts to fill in a current list of visited vertices. Like so:

void allPaths(vector<int> previous, int current, int destination)
{
    previous.push_back(current);

    if (current == destination)
        //output all elements of previous, and return

    for (int i = 0; i < neighbors[current].size(); i++)
        allPaths(previous, neighbors[current][i], destination);
}

int main()
{
    //...input
    allPaths(vector<int>(), start, end);
}

Due to the fact that the vector is passed by value (and thus any changes made further down in the recursive procedure aren't permanent), all possible combinations are enumerated.

You can gain a bit of efficiency by passing the previous vector by reference (and thus not needing to copy the vector over and over again) but you'll have to make sure that things get popped_back() manually.

One more thing: if the graph has cycles, this won't work.
(I assume in this case you'll want to find all simple paths, then) Before adding something into the previous vector, first check if it's already in there.

If you want all shortest paths, use Konrad's suggestion with this algorithm.

回复 原文
绝對不後悔。 2024-07-23 06:35:08

给定邻接矩阵：

{0, 1, 3, 4, 0, 0}

{0, 0, 2, 1, 2, 0}

{0, 1, 0, 3, 0, 0}

{0, 1, 1 , 0, 0, 1}

{0, 0, 0, 0, 0, 6}

{0, 1, 0, 1, 0, 0}

以下 Wolfram Mathematica 代码解决了查找两个节点之间所有简单路径的问题的图表。
我使用简单的递归和两个全局变量来跟踪循环并存储所需的输出。
代码并没有仅仅为了代码的清晰度而进行优化。
“打印”应该有助于阐明它是如何工作的。

cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True];
getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]];

builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos},
    If[{node} != {} && node != endNode ,
        root = node;
        nodes = getNode[matrix, node];
        (*Print["root:",root,"---nodes:",nodes];*)

        AppendTo[lcycle, Flatten[{root, nodes}]];
        If[cycleQ[lcycle] == True,
            lcycle = Most[lcycle]; appendToTree[root, nodes];,
            Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes];
            appendToTree[root, nodes];

        ];
    ];

appendToTree[root_, nodes_] := Block[{pos, toAdd},
    pos = Flatten[Position[tree[[All, -1]], root]];
    For[i = 1, i <= Length[pos], i++,
        toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes;
        (* check cycles!*)            
        If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd;
    ];
    tree = Delete[tree, {#} & /@ pos];
    builtTree[#, matrix] & /@ Union[tree[[All, -1]]];
    ];
];

调用代码：
初始化节点=1；
结束节点 = 6;
循环={};
树= {{initNode}};
builtTree[initNode, 矩阵];

路径：{{1}}
root:1---节点:{2,3,4}

路径: {{1,2},{1,3},{1,4}}
root:2---节点:{3,4,5}

路径：{{1,3},{1,4},{1,2,3},{1,2,4},{1,2 ,5}}
根：3---节点：{2,4}

路径：{{1,4},{1,2,4},{1,2,5},{1,3,4},{1,2 ,3,4},{1,3,2,4},{1,3,2,5}}
root:4---节点:{2,3,6}

路径:{{1,2,5},{1,3,2,5},{1,4,6},{1,2,4 ,6},{1,3,4,6},{1,2,3,4,6},{1,3,2,4,6},{1,4,2,5},{1 ,3,4,2,5},{1,4,3,2,5}}
根:5---节点:{6}

结果:{{1, 4, 6}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 6 }, {1, 2, 3, 4, 6}, {1, 3, 2, 4, 6}, {1, 3, 2, 5, 6}, {1, 4, 2, 5, 6}, {1, 3, 4, 2, 5, 6}, {1, 4, 3, 2, 5, 6}}

...不幸的是，我无法上传图像以更好的方式显示结果:(

http://textanddatamining.blogspot.com

given the adjacency matrix:

{0, 1, 3, 4, 0, 0}

{0, 0, 2, 1, 2, 0}

{0, 1, 0, 3, 0, 0}

{0, 1, 1, 0, 0, 1}

{0, 0, 0, 0, 0, 6}

{0, 1, 0, 1, 0, 0}

the following Wolfram Mathematica code solve the problem to find all the simple paths between two nodes of a graph.
I used simple recursion, and two global var to keep track of cycles and to store the desired output.
the code hasn't been optimized just for the sake of code clarity.
the "print" should be helpful to clarify how it works.

cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True];
getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]];

builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos},
    If[{node} != {} && node != endNode ,
        root = node;
        nodes = getNode[matrix, node];
        (*Print["root:",root,"---nodes:",nodes];*)

        AppendTo[lcycle, Flatten[{root, nodes}]];
        If[cycleQ[lcycle] == True,
            lcycle = Most[lcycle]; appendToTree[root, nodes];,
            Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes];
            appendToTree[root, nodes];

        ];
    ];

appendToTree[root_, nodes_] := Block[{pos, toAdd},
    pos = Flatten[Position[tree[[All, -1]], root]];
    For[i = 1, i <= Length[pos], i++,
        toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes;
        (* check cycles!*)            
        If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd;
    ];
    tree = Delete[tree, {#} & /@ pos];
    builtTree[#, matrix] & /@ Union[tree[[All, -1]]];
    ];
];

to call the code:
initNode = 1;
endNode = 6;
lcycle = {};
tree = {{initNode}};
builtTree[initNode, matrix];

paths: {{1}}
root:1---nodes:{2,3,4}

paths: {{1,2},{1,3},{1,4}}
root:2---nodes:{3,4,5}

paths: {{1,3},{1,4},{1,2,3},{1,2,4},{1,2,5}}
root:3---nodes:{2,4}

paths: {{1,4},{1,2,4},{1,2,5},{1,3,4},{1,2,3,4},{1,3,2,4},{1,3,2,5}}
root:4---nodes:{2,3,6}

paths: {{1,2,5},{1,3,2,5},{1,4,6},{1,2,4,6},{1,3,4,6},{1,2,3,4,6},{1,3,2,4,6},{1,4,2,5},{1,3,4,2,5},{1,4,3,2,5}}
root:5---nodes:{6}

RESULTS:{{1, 4, 6}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 6}, {1, 2, 3, 4, 6}, {1, 3, 2, 4, 6}, {1, 3, 2, 5, 6}, {1, 4, 2, 5, 6}, {1, 3, 4, 2, 5, 6}, {1, 4, 3, 2, 5, 6}}

...Unfortunately I cannot upload images to show the results in a better way :(

http://textanddatamining.blogspot.com

回复 原文
我只土不豪 2024-07-23 06:35:08

您要做的本质上是在（有向？）图中找到两个顶点之间的路径，请查看 Dijkstra 算法，如果您需要最短路径，或者编写一个简单的递归函数，如果您需要任何存在的路径。

What you're trying to do is essentially to find a path between two vertices in a (directed?) graph check out Dijkstra's algorithm if you need shortest path or write a simple recursive function if you need whatever paths exist.

回复 原文
~没有更多了~

关于作者

嘿嘿嘿

暂无简介

文章
评论
25 人气
发私信

相关话题

更多

热门标签

操作系统 程序设计 IT运维 Linux系统管理 JavaScript 服务器应用 solaris C/C++ PHP Shell BSD Vue.js aix Oracle Python HTML 系统管理 HTML5 CSS 前端
更多

推荐作者

Promise

文章 0 评论 0

qq_lbRlsh

文章 0 评论 0

待＂谢繁草

文章 0 评论 0

yy2010hell

文章 0 评论 0

漫无边际

文章 0 评论 0

傲娇萝莉攻

文章 0 评论 0

更多

友情链接

文江博客
    我们使用 Cookies 和其他技术来定制您的体验包括您的登录状态等。通过阅读我们的 隐私政策 了解更多相关信息。 单击 接受 或继续使用网站，即表示您同意使用 Cookies 和您的相关数据。
    原文