生成字符串所有可能排列的列表
我将如何生成长度为 x 和 y 字符之间的字符串的所有可能排列的列表,其中包含可变字符列表。
任何语言都可以,但它应该是可移植的。
How would I go about generating a list of all possible permutations of a string between x and y characters in length, containing a variable list of characters.
Any language would work, but it should be portable.
如果你对这篇内容有疑问,欢迎到本站社区发帖提问 参与讨论,获取更多帮助,或者扫码二维码加入 Web 技术交流群。

绑定邮箱获取回复消息
由于您还没有绑定你的真实邮箱,如果其他用户或者作者回复了您的评论,将不能在第一时间通知您!

发布评论
评论(30)
根据 Knuth、Python 示例的非递归解决方案:
Non recursive solution according to Knuth, Python example:
您可以查看“高效枚举集合的子集”,它描述了一种执行部分操作的算法您想要的内容 - 快速生成长度为 x 到 y 的 N 个字符的所有子集。 它包含 C 语言的实现。
对于每个子集,您仍然必须生成所有排列。 例如,如果您想要“abcde”中的 3 个字符,该算法将为您提供“abc”、“abd”、“abe”...
但你必须对每一个进行排列才能得到“acb”、“bac”、“bca”等。
You might look at "Efficiently Enumerating the Subsets of a Set", which describes an algorithm to do part of what you want - quickly generate all subsets of N characters from length x to y. It contains an implementation in C.
For each subset, you'd still have to generate all the permutations. For instance if you wanted 3 characters from "abcde", this algorithm would give you "abc","abd", "abe"...
but you'd have to permute each one to get "acb", "bac", "bca", etc.
一些基于 Sarp 的回答:
Some working Java code based on Sarp's answer:
你会得到很多字符串,这是肯定的...
其中 x 和 y 是您定义它们的方式,r 是我们从中选择的字符数 - 如果我理解正确的话。 您绝对应该根据需要生成这些,而不是马虎地说,生成一个幂集,然后过滤字符串的长度。
以下绝对不是生成这些的最佳方法,但它仍然是一个有趣的旁白。
Knuth(第 4 卷,分册 2,7.2.1.3)告诉我们,(s,t)-组合相当于每次重复 t 取 s+1 个事物——(s,t)-组合是Knuth 等于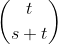 。 我们可以通过首先以二进制形式生成每个 (s,t) 组合(因此长度为 (s+t))并计算每个 1 左侧 0 的数量来计算出这一点。
。 我们可以通过首先以二进制形式生成每个 (s,t) 组合(因此长度为 (s+t))并计算每个 1 左侧 0 的数量来计算出这一点。
10001000011101 --> 变为排列:{0, 3, 4, 4, 4, 1}
You are going to get a lot of strings, that's for sure...
Where x and y is how you define them and r is the number of characters we are selecting from --if I am understanding you correctly. You should definitely generate these as needed and not get sloppy and say, generate a powerset and then filter the length of strings.
The following definitely isn't the best way to generate these, but it's an interesting aside, none-the-less.
Knuth (volume 4, fascicle 2, 7.2.1.3) tells us that (s,t)-combination is equivalent to s+1 things taken t at a time with repetition -- an (s,t)-combination is notation used by Knuth that is equal to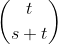 . We can figure this out by first generating each (s,t)-combination in binary form (so, of length (s+t)) and counting the number of 0's to the left of each 1.
. We can figure this out by first generating each (s,t)-combination in binary form (so, of length (s+t)) and counting the number of 0's to the left of each 1.
10001000011101 --> becomes the permutation: {0, 3, 4, 4, 4, 1}
最好使用回溯
It's better to use backtracking
这是 Mike 的 Ruby 版本到 Common Lisp 的翻译:
另一个版本稍短并使用更多循环设施功能:
This is a translation of Mike's Ruby version, into Common Lisp:
And another version, slightly shorter and using more loop facility features:
我刚刚在 Ruby 中快速完成了这个:
您可能会研究内置排列类型函数的语言 API,并且您可能能够编写更优化的代码,但如果数字都那么高,我不确定有多少一种获得大量结果的方法。
无论如何,代码背后的想法是从长度为 0 的字符串开始,然后跟踪长度为 Z 的所有字符串,其中 Z 是迭代中的当前大小。 然后,遍历每个字符串并将每个字符附加到每个字符串上。 最后,删除任何低于 x 阈值的值并返回结果。
我没有使用可能无意义的输入(空字符列表、奇怪的 x 和 y 值等)来测试它。
I just whipped this up quick in Ruby:
You might look into language API for built in permutation type functions, and you might be able to write more optimized code, but if the numbers are all that high, I'm not sure there is much of a way around having a lot of results.
Anyways, the idea behind the code is start with string of length 0, then keep track of all the strings of length Z where Z is the current size in the iteration. Then, go through each string and append each character onto each string. Finally at the end, remove any that were below the x threshold and return the result.
I didn't test it with potentially meaningless input (null character list, weird values of x and y, etc).
这里有很多好的答案。 我还建议在 C++ 中使用一个非常简单的递归解决方案。
注意:具有重复字符的字符串不会产生唯一的排列。
There are a lot of good answers here. I also suggest a very simple recursive solution in C++.
Note: strings with repeated characters will not produce unique permutations.
这是 C# 中的一个简单解决方案。
它仅生成给定字符串的不同排列。
Here is a simple solution in C#.
It generates only the distinct permutations of a given string.
这是一个描述如何打印字符串排列的链接。
http://nipun-linuxtips.blogspot .in/2012/11/print-all-permutations-of-characters-in.html
Here is a link that describes how to print permutations of a string.
http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html
python 中的这段代码,当调用
allowed_characters设置为[0,1]且最多 4 个字符时,将生成 2^4 个结果:['0000', ‘0001’、‘0010’、‘0011’、‘0100’、‘0101’、‘0110’、‘0111’、‘1000’、‘1001’、‘1010’、‘1011’、‘1100’、‘1101 ', '1110', '1111']希望这对您有用。 适用于任何字符,而不仅仅是数字
This code in python, when called with
allowed_charactersset to[0,1]and 4 character max, would generate 2^4 results:['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']Hope this is of use to you. Works with any character, not only numbers
之前的很多答案都使用了回溯。 这是初始排序后生成排列的渐近最优方式 O(n*n!)
Many of the previous answers used backtracking. This is the asymptotically optimal way O(n*n!) of generating permutations after initial sorting
递归方法
Recursive Approach
虽然这并不能完全回答你的问题,但这里有一种方法可以从多个相同长度的字符串中生成字母的每种排列:例如,如果你的单词是“coffee”、“joomla”和“moodle”,你可以期望输出像“coodle”、“joodee”、“joffle”等。
基本上,组合的数量是(单词数)的(每个单词的字母数)次方。 因此,在 0 和组合数 - 1 之间选择一个随机数,将该数字转换为基数(单词数),然后使用该数字的每个数字作为从哪个单词获取下一个字母的指示符。
例如:在上面的例子中。 3 个单词,6 个字母 = 729 种组合。 选择一个随机数:465。转换为基数 3:122020。从单词 1 中取出第一个字母,从单词 2 中取出第二个字母,从单词 2 中取出第三个,从单词 0 中取出第四个......然后你得到......“joofle”。
如果您想要所有的排列,只需从 0 到 728 循环即可。当然,如果您只是选择一个随机值,一种
更简单不太令人困惑的方法是循环遍历字母。 如果您想要所有排列,此方法可以让您避免递归,而且它让您看起来像知道数学(tm)!如果组合数量过多,您可以将其分解为一系列较小的单词并在最后将它们连接起来。
Though this doesn't answer your question exactly, here's one way to generate every permutation of the letters from a number of strings of the same length: eg, if your words were "coffee", "joomla" and "moodle", you can expect output like "coodle", "joodee", "joffle", etc.
Basically, the number of combinations is the (number of words) to the power of (number of letters per word). So, choose a random number between 0 and the number of combinations - 1, convert that number to base (number of words), then use each digit of that number as the indicator for which word to take the next letter from.
eg: in the above example. 3 words, 6 letters = 729 combinations. Choose a random number: 465. Convert to base 3: 122020. Take the first letter from word 1, 2nd from word 2, 3rd from word 2, 4th from word 0... and you get... "joofle".
If you wanted all the permutations, just loop from 0 to 728. Of course, if you're just choosing one random value, a much
simplerless-confusing way would be to loop over the letters. This method lets you avoid recursion, should you want all the permutations, plus it makes you look like you know Maths(tm)!If the number of combinations is excessive, you can break it up into a series of smaller words and concatenate them at the end.
时间:2019-03-17 标签:c#iterative
c# iterative:
这是我对非递归版本的看法
Here is my take on a non recursive version
我今天需要这个,尽管已经给出的答案为我指明了正确的方向,但它们并不是我想要的。
这是使用Heap方法的实现。 数组的长度必须至少为 3,出于实际考虑,不能大于 10 左右,具体取决于您想要做什么、耐心和时钟速度。
在进入循环之前,请使用第一个排列初始化
Perm(1 To N)、使用零*初始化Stack(3 To N)和Level与2**。 在循环结束时调用NextPerm,完成后将返回 false。* VB 会为你做这件事。
** 你可以稍微改变 NextPerm 来使这个变得不必要,但这样更清晰。
不同的作者描述了其他方法。 高德纳描述了两种,一种给出了词汇顺序,但复杂且缓慢,另一种被称为简单变化的方法。 高杰和王殿军也写了一篇有趣的论文。
I needed this today, and although the answers already given pointed me in the right direction, they weren't quite what I wanted.
Here's an implementation using Heap's method. The length of the array must be at least 3 and for practical considerations not be bigger than 10 or so, depending on what you want to do, patience and clock speed.
Before you enter your loop, initialise
Perm(1 To N)with the first permutation,Stack(3 To N)with zeroes*, andLevelwith2**. At the end of the loop callNextPerm, which will return false when we're done.* VB will do that for you.
** You can change NextPerm a little to make this unnecessary, but it's clearer like this.
Other methods are described by various authors. Knuth describes two, one gives lexical order, but is complex and slow, the other is known as the method of plain changes. Jie Gao and Dianjun Wang also wrote an interesting paper.
下面是一个简单的 C# 单词递归解决方案:
方法:
调用:
Here is a simple word C# recursive solution:
Method:
Calling:
...这是 C 版本:
... and here is the C version:
打印所有无重复项的排列
Prints all permutations sans duplicates
C++中的递归解决方案
Recursive solution in C++
在 Perl 中,如果您想将自己限制为小写字母,您可以这样做:
这将使用小写字符给出 1 到 4 个字符之间的所有可能字符串。 对于大写字母,请将
"a"更改为"A",将"zzzz"更改为"ZZZZ"。对于混合大小写,它会变得更加困难,并且可能无法使用像这样的 Perl 内置运算符之一来实现。
In Perl, if you want to restrict yourself to the lowercase alphabet, you can do this:
This gives all possible strings between 1 and 4 characters using lowercase characters. For uppercase, change
"a"to"A"and"zzzz"to"ZZZZ".For mixed-case it gets much harder, and probably not doable with one of Perl's builtin operators like that.
有效的 Ruby 答案:
Ruby answer that works:
以下 Java 递归打印给定字符串的所有排列:
以下是上述“permut”方法的更新版本,该方法使 n! 与上述方法相比,(n 阶乘)递归调用更少
The following Java recursion prints all permutations of a given string:
Following is the updated version of above "permut" method which makes n! (n factorial) less recursive calls compared to the above method
我不确定你为什么要这样做。 任何中等大的 x 和 y 值的结果集都将是巨大的,并且随着 x 和/或 y 变大而呈指数增长。
假设您的可能字符集是字母表中的 26 个小写字母,并且您要求应用程序生成长度 = 5 的所有排列。假设您没有耗尽内存,您将得到 11,881,376(即 26 次方) 5) 弦背。 将长度增加到 6,您将得到 308,915,776 个字符串。 这些数字很快就会变得非常大。
这是我用 Java 编写的一个解决方案。 您需要提供两个运行时参数(对应于 x 和 y)。 玩得开心。
I'm not sure why you would want to do this in the first place. The resulting set for any moderately large values of x and y will be huge, and will grow exponentially as x and/or y get bigger.
Lets say your set of possible characters is the 26 lowercase letters of the alphabet, and you ask your application to generate all permutations where length = 5. Assuming you don't run out of memory you'll get 11,881,376 (i.e. 26 to the power of 5) strings back. Bump that length up to 6, and you'll get 308,915,776 strings back. These numbers get painfully large, very quickly.
Here's a solution I put together in Java. You'll need to provide two runtime arguments (corresponding to x and y). Have fun.
这是我用 javascript 提出的非递归版本。
它不是基于上面 Knuth 的非递归非递归,尽管它在元素交换方面有一些相似之处。
我已经验证了最多 8 个元素的输入数组的正确性。
快速优化是预先处理
out数组并避免push()。基本思想是:
给定一个源数组,生成第一组新数组,依次将第一个元素与每个后续元素交换,每次都保持其他元素不受干扰。
例如:给定 1234,生成 1234, 2134, 3214, 4231。
使用上一次传递中的每个数组作为新传递的种子,
但不是交换第一个元素,而是将第二个元素与每个后续元素交换。 另外,这一次,不要在输出中包含原始数组。
重复步骤 2 直至完成。
这是代码示例:
Here's a non-recursive version I came up with, in javascript.
It's not based on Knuth's non-recursive one above, although it has some similarities in element swapping.
I've verified its correctness for input arrays of up to 8 elements.
A quick optimization would be pre-flighting the
outarray and avoidingpush().The basic idea is:
Given a single source array, generate a first new set of arrays which swap the first element with each subsequent element in turn, each time leaving the other elements unperturbed.
eg: given 1234, generate 1234, 2134, 3214, 4231.
Use each array from the previous pass as the seed for a new pass,
but instead of swapping the first element, swap the second element with each subsequent element. Also, this time, don't include the original array in the output.
Repeat step 2 until done.
Here is the code sample:
在 ruby 中:
速度相当快,但需要一些时间 =)。 当然,如果您对短字符串不感兴趣,您可以从“aaaaaaaa”开始。
不过,我可能误解了实际的问题 - 在其中一篇文章中,听起来好像您只需要一个强力字符串库,但在主要问题中,听起来您需要排列特定的字符串。
您的问题与此有点相似: http://beust.com/weblog/archives/000491 .html (列出所有没有数字重复的整数,这导致了很多语言解决这个问题,ocaml 人员使用排列,而一些 java 人员使用另一种解决方案)。
In ruby:
It is quite fast, but it is going to take some time =). Of course, you can start at "aaaaaaaa" if the short strings aren't interesting to you.
I might have misinterpreted the actual question though - in one of the posts it sounded as if you just needed a bruteforce library of strings, but in the main question it sounds like you need to permutate a particular string.
Your problem is somewhat similar to this one: http://beust.com/weblog/archives/000491.html (list all integers in which none of the digits repeat themselves, which resulted in a whole lot of languages solving it, with the ocaml guy using permutations, and some java guy using yet another solution).
做这件事有很多种方法。 常见的方法使用递归、记忆或动态编程。 基本思想是,生成长度为 1 的所有字符串的列表,然后在每次迭代中,对于上次迭代中生成的所有字符串,分别添加与字符串中的每个字符连接的字符串。 (下面代码中的变量索引跟踪上一次和下一次迭代的开始)
一些伪代码:
然后您需要删除长度小于 x 的所有字符串,它们将是第一个 (x-1) * 列表中的 len(originalString) 条目。
There are several ways to do this. Common methods use recursion, memoization, or dynamic programming. The basic idea is that you produce a list of all strings of length 1, then in each iteration, for all strings produced in the last iteration, add that string concatenated with each character in the string individually. (the variable index in the code below keeps track of the start of the last and the next iteration)
Some pseudocode:
you'd then need to remove all strings less than x in length, they'll be the first (x-1) * len(originalString) entries in the list.